自然換気量の計算法 [多重開口の場合]
2022-04-01建物の開口部で生じる自然換気量は、下記の式[1]を用いて計算される。
Q = \alpha A\sqrt{\frac{2 \Delta P}{\rho}} \; \cdots \; [1]ここで、Q [m3/s]は換気量、α [-]は流量係数、A [m2]は開口面積、ρ [kg/m3]は流体密度（空気の場合は、約1.2 kg/m3）、ΔP [Pa]は室内外圧力差である。
式[1]によると自然換気量は、室内外圧力差 ΔP（風圧差 ΔPw か温度差 ΔT ）と、開口における流量係数 α（圧力損失係数 ξの平方根の逆数）に比例する形で計算される。以下では、流量係数 α、有効開口面積 αAについてそれぞれ概説し、風圧差 ΔPwか温度差 ΔT によって発生する自然換気（風力換気／温度差換気）による自然換気量の計算法について説明する。
※ 多重開口ではなく、単一開口における自然換気量の計算法は計算原理が異なるため、下記のブログをご確認ください。
https://lee-lab.net/blog-contents-004
【1】流量係数（α）
空気が開口部を通過する際には、開口部の形状、材質、長さ、空気の流速などの要因により抵抗が生じ、その結果として空気の圧力が低下する。この現象は「圧力損失」と呼ばれる。この圧力損失の大きさを開口部を通過する気流速度（Uo）や密度（ρ）に依存しない形で比較するために、圧力損失（ΔP）を動圧（Pv）で割った無次元数が一般的に用いられる。これを「圧力損失係数」と呼び、式[2]に示すように 記号 ξ [-]で表される。
\xi = \frac{{\Delta}{P}}{P_{v}} = \frac{{\Delta}{P}}{ \frac{{1}}{{2}} \rho U_{o}^{2}} = \frac{{\Delta}{P}}{ \frac{{1}}{{2}} \rho \left ( {Q_{r}}/{A} \right )^{2}} \; \cdots \; [2]ここで、Pv [Pa]は動圧、Uo [m/s]は開口部を通過する気流速度（代表速度）、Qr [m3/s]は実際の流量または実測流量である。
一方、流量係数 αは、開口部を通過する実際の流量と、圧力損失がない理想状態で得られる理論流量と比（式[3]参照）として定義され、圧力損失係数 ξの平方根の逆数に相当する。
\alpha = \frac{{Q}_{r}}{A \sqrt {\frac{{2}\Delta{P}}{\rho}}} = \frac{{1}}{{\sqrt{\xi}}} \; \cdots \; [3]図1に、様々な開口部における典型的な流量係数を示す。例えば、通常の窓は0.6～0.7程度であるが、ベルマウス形状のように入口形状がスムーズな場合、流れの縮流や剥離が抑えられ、流量係数は概ね1となる。また、ルーバーが設置される場合はその角度によって圧力損失が変わるため、角度によって異なる。開き窓の場合、開き角度によって変わる流量係数を図2に示す。また、網戸、カーテン、ブラインドなどを使用する場合にも圧力損失が生じるため、適正な流量係数を計測して適用する必要がある。
図1. 開口部における流量係数
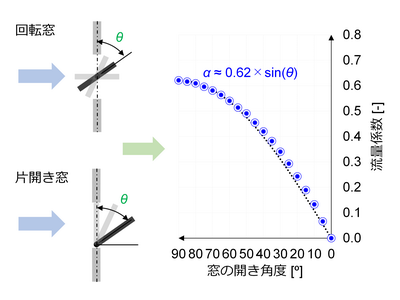図2. 窓の開き角度による流量係数
(Calculated by Akane Tsutsumi et al. [PDF])
【2】有効開口面積（αA）
有効開口面積（αA）は開口配置によって並列合成と直列合成に分けて計算でき、それぞれ式[7]と式[11]で計算される。
① αA の並列合成
有効開口面積（αA）の並列合成は図3に示したものであり、開口部1と2の前後に作用する全圧PTa とPTb が等しいとしてαA合値を計算する。
図3. αAの並列合成
Q_{1} = \alpha_{1} A_{1} \sqrt{ \frac{{2}{\Delta}{P}}{\rho} } \; \cdots \; [4]Q_{2} = \alpha_{2} A_{2} \sqrt{ \frac{{2}{\Delta}{P}}{\rho} } \; \cdots \; [5]\def\arraystretch{1.2}\begin{aligned} Q & = Q_{1}+Q_{2} \\\ &= (\alpha_{1} A_{1}+\alpha_{2} A_{2}) \sqrt{ \frac{{2}{\Delta}{P}}{\rho} }
\; \cdots \; [6]
\end{aligned} \alpha A_{合} = \alpha_{1} A_{1} + \alpha_{2} A_{2} \; \cdots \; [7]② αA の直列合成
有効開口面積（αA）の直列合成は図4に示したものであり、開口部1と2を通過する風量 Q が等しいとして αA合値を計算する。
図4. αA の直列合成
Q = \alpha_{1} A_{1} \sqrt{ \frac{{2}{\Delta}{P_{a} }}{\rho} } = \alpha_{2} A_{2} \sqrt{ \frac{{2}{\Delta}{P_{b} }}{\rho} } \; \cdots \; [8]\def\arraystretch{1.5}\begin{aligned}
\Delta P & = \Delta P_{a} + \Delta P_{b} \\
& = \frac{1}{2} \rho \left(\frac{Q}{\alpha_{1} A_{1}} \right)^{2} + \frac{1}{2} \rho \left(\frac{Q}{\alpha_{2} A_{2}} \right)^{2}
\; \cdots \; [9]
\end{aligned}Q =\frac{1}{\sqrt {\left(\frac{1}{\alpha_{1} A_{1}} \right)^{2} + \left(\frac{1}{\alpha_{2} A_{2}} \right)^{2}}} \sqrt{ \frac{{2}{\Delta}{P}}{\rho} } \; \cdots \; [10]\alpha A_{合} = \frac{1}{\sqrt {\left(\frac{1}{\alpha_{1} A_{1}} \right)^{2} + \left(\frac{1}{\alpha_{2} A_{2}} \right)^{2}}} \; \cdots \; [11]【3】風力換気
建物に風が吹き付けると、大気圧に風圧力が加算されて作用する。図5に示すように風上側に掛かって来る風圧 Pw [Pa]は、基準風速 （軒高風速が基準）U [m/s]と風圧係数 Cw [-]を用いて式[12]で計算される。
図5. 風力による圧力差
P_{\mathrm{w}} = C_{\mathrm{w}}\frac{1}{2}\rho_{\mathrm{o}}U^{2} \; \cdots \; [12]ここで、Pw [Pa]は風圧、Cw [-]は風圧係数、ρo [kg/m3]は外気密度、U [m/s]は基準風速である。
開口部がある建物に風が吹き付けると、図6に示すように風上側に掛かって来る風圧 Pw1 [Pa]と風下側の風圧 Pw2 [Pa]の差 ΔP [Pa]は、基準風速 U [m/s]と風圧係数 Cw1 [-]と Cw2 [-]の差 (Cw1 – Cw2) [-]を用いて式[13]で計算できる。
図6. 風力による圧力差
\Delta P = \left ( C_{\mathrm{w1}}-C_{\mathrm{w2}} \right )\frac{1}{2}\rho_{\mathrm{o}}U^{2} \; \cdots \; [13]ここで、ΔP [Pa]は風圧Pw1 [Pa]と風圧Pw2 [Pa]の差圧、Cw1 [-]は風上側の風圧係数、Cw2 [-]は風下側の風圧係数、ρo [kg/m3]は外気密度、U [m/s]は基準風速である。
式[13]を式[1]に代入して整理すると、風力による換気量 Qは式[14]で計算できる。
Q = \alpha A_{合} \cdot U \cdot \sqrt{C_{\mathrm{w1}}-C_{\mathrm{w2}} } \; \cdots \; [14]一方、風圧係数は実測、模型を用いた風洞実験（図7参照）によって測定値を用いるか、それとも推定式、CFD解析などによる計算値を使う場合もある。図8、図9にAkinsら（1979）1[1] Akins, R.E., J.A. Peterka, and J.E. Cermak. 1979. Averaged pressure coefficients for rectangular buildings. Wind Engineering: Proceedings of the Fifth International Conference, vol. 7, pp. 369-380.が高層ビルを対象として行った風洞実験の壁面、屋根面の結果値を示し、図10には低層ビルに対してSwamiら（1987）2[2] Swami, M.V., and S. Chandra. 1987. Procedures for calculating natural ventilation airflow rates in buildings. Final Report FSEC-CR-163-86. Florida Solar Energy Center, Cape Canaveral.が報告した風圧係数を示す。
図7. 模型を用いた風洞実験による風圧係数
図8. 壁面における風圧係数（Akins et al.）
図9. 屋根面における風圧係数（Akins et al.）
図10. 壁面における風圧係数（Swami et al.）
また、Walkerら（1994）3[3] Walker, I.S., and D.J. Wilson. 1994. Practical methods for improving estimates of natural ventilation rates. Proceedings of the 15th IEA Conference of the Air Infiltration and Ventilation Centre, Buxton, U.K., pp. 517-526.は、風の風向角による風圧係数の推定式を式[15]のように提案している。
\def\arraystretch{1.5}\begin{aligned}
{C}_{\textrm{p}}(\phi) = & 1/2 \{ [{{C}_{\textrm{p}}(1)}+{{C}_{\textrm{p}}(2)}](cos^{2}\phi)^{1/4} \\\
& +
[{{C}_{\textrm{p}}(1)}-{{C}_{\textrm{p}}(2)}](cos\phi)^{3/4} \\\
& +
[{{C}_{\textrm{p}}(3)}+{{C}_{\textrm{p}}(4)}](sin^{2}\phi)^{2} \\\
& +
[{{C}_{\textrm{p}}(3)}-{{C}_{\textrm{p}}(4)}]sin\phi \}
\end{aligned}
\; \cdots \; [15]ここで、Cp(1) は風向0°での風圧係数、Cp(2) は風向180°での風圧係数、Cp(3) は風向90°での風圧係数、Cp(4) は風向270°での風圧係数、φ は壁面に対して時計回り風向角である。
【4】温度差換気
図11に示すように、建物において上下2か所に開口部があり、室内温度が室外温度よりも高い場合、室内では上昇気流が生じる。この現象を温度差換気（stack ventilation）と呼び、その換気量は以下の式[16]で室内外圧力差を求め、式[1]に代入することで算出できる。
\Delta P = \Delta \rho g h \; \cdots \; [16]
ここで、ΔP [Pa]は開口部1における風圧P1 [Pa]と開口部2における風圧P2 [Pa]の差圧、Δρ [kg/m3]は室外の空気密度ρo [kg/m3]と室内の空気密度ρi [kg/m3]の密度差、g [m/s2]は重力加速度、h [m]は開口間の高さである。
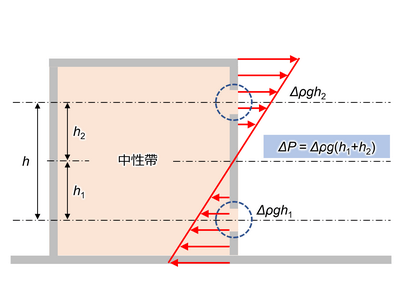図11. 温度差による圧力差
式[16]における室内外密度差Δρは、式[17]に示すシャルル法則（Charles’ law）によって室外温度Ti [K]と室内外温度差ΔT [K]に変換でき、式[18]のように表される。
\rho_{\mathrm{o}} T_{\mathrm{o}} = \rho_{\mathrm{i}} T_{\mathrm{i}} \; \cdots \; [17]\begin{aligned}
\Delta \rho & = \rho_{\mathrm{o}} - \rho_{\mathrm{i}} = \rho_{\mathrm{o}} - \frac{\rho_{\mathrm{o}}T_{\mathrm{o}}}{T_{\mathrm{i}}} \\\
& = \frac{\rho_{\mathrm{o}}(T_{\mathrm{i}} - T_{\mathrm{o}})}{T_{\mathrm{i}}} = \frac{\rho_{\mathrm{o}}\Delta T}{T_{\mathrm{i}}} \; \cdots \; [18]
\end{aligned}ここで、ΔT [K]は室内温度Ti [K]と室外温度To [K]の室内外温度差である。
式[18]を式[16]に代入して整理すると、室内外温度差ΔTによる室内外圧力差ΔPは式[19]のように表される。
\Delta P = \Delta \rho g h = \frac{\rho_{\mathrm{o}}\Delta Tgh}{T_{\mathrm{i}}} \; \cdots \; [19]式[19]を式[1]に代入して整理すると、室内外温度差ΔTによる換気量 Qは式[20]のようになる。
Q = \alpha A_{合} \cdot \sqrt{\frac{2 \cdot \Delta Tgh}{T_{\mathrm{i}}} } \; \cdots \; [20]| ※ 開口部が一箇所の建物では開口部での大気基準圧は0となり、それ以上では正圧（図12参照）となる。ここで大気基準圧とは、同一高度の大気圧を基準とした圧力表示を大気基準圧と言う。 |
 図12. 開口部が一箇所の建物 |
| また、上部にも開口部ができると、上部では正圧、下部では負圧となる分布が形成され、上部で室空気が流出し、下部から流入（図13参照）する。 |
 図13. 開口部が二箇所の建物 |
| 一方、中性帯の高さは、開口部の有効開口面積（αA）が同じであれば中立位置に形成されるが、開口部の有効開口面積が異なるとαAが大きい方（図14参照）に近づく。 |
 図14. 開口部の有効開口面積（αA）と中性帯高さの関係 |
一方、温度差換気において、開口部における圧力損失の計算（式[1]）に用いる密度（ρ）は、厳密には開口部ことに異なる密度（ρiやρo）を用いるべきだが、実務や教育現場では簡略化の一環として室内外で区分せず、ρ ≈ ρoと仮定すること（式[21]参照）が一般的である。これは、室内外の温度差（ΔT）が小さい範囲では室内外の密度差（Δρ）も小さく、換気量の計算精度に大きな影響を与えないためである。
Q = \alpha A_{合} \cdot \sqrt{\frac{2 \cdot \textcolor{red}{\Delta \rho} gh}{\textcolor{red}{\rho_{\mathrm{o}}} } } \approx \alpha A_{合} \cdot \sqrt{\frac{2 \cdot \Delta Tgh}{T_{\mathrm{i}}} } \; \cdots \; [21]室内外の密度差（Δρ/ρo）それとも室内外の温度差（ΔT/To）が大きい時に発生する換気量の誤差を推定するためには、以下に示す簡単な計算から推定可能である。
図15に示すように2つの開口部（αA）を持つ建物における温度差のみの自然換気を考える。
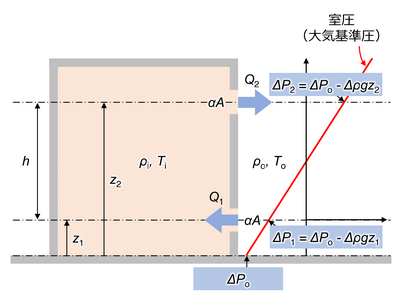図15. 温度差による圧力差
この場合、連続の式は式[22]と示され、各開口部における風量はそれぞれ式[23]、式[24]から求められる。
\rho_{\mathrm{o}} Q_{\mathrm{1}}' + \rho_{\mathrm{i}} Q_{\mathrm{2}}' = 0 \; \cdots \; [22]Q_{\mathrm{1}}' = \alpha A \cdot \sqrt{\frac{2 \cdot \Delta P_{\mathrm{1}}}{\rho_{\mathrm{o}}} } \; \cdots \; [23]Q_{\mathrm{2}}' = \alpha A \cdot \sqrt{\frac{-2 \cdot \Delta P_{\mathrm{2}}}{\rho_{\mathrm{i}}} } \; \cdots \; [24]ここで、ΔP₁、ΔP₂は各開口部がある高さz₁、z₂における圧力差であり、以下の式[25]、式[26]のように表される。
\Delta P_{\mathrm{1}} = \Delta P_{\mathrm{o}} - \Delta \rho g z_{\mathrm{1}} \; \cdots \; [25]\Delta P_{\mathrm{2}} = \Delta P_{\mathrm{o}} - \Delta \rho g z_{\mathrm{2}} \; \cdots \; [26]ここで、Δρ ≡ ρₒ – ρᵢである。
換気量の誤差を推定するために、以上の関係から式を纏めて整理すると、各開口部における風量はそれぞれ式[27]、式[28]のように表される。
Q_{\mathrm{1}}' = \alpha A \cdot \sqrt{\frac{\Delta \rho g h}{\rho_{\mathrm{o}}} } \sqrt{ \frac{2 \cdot \rho_{\mathrm{i}} } {(\rho_{\mathrm{o}} + \rho_{\mathrm{i}})} } \; \cdots \; [27]Q_{\mathrm{2}}' = \alpha A \cdot \sqrt{\frac{\Delta \rho g h}{\rho_{\mathrm{o}}} } \sqrt{ \frac{2 \cdot \rho_{\mathrm{i}}^2 } {\rho_{\mathrm{i}}(\rho_{\mathrm{o}} + \rho_{\mathrm{i}})} } \; \cdots \; [28]室内外の空気密度が等しい（ρi = ρo）と仮定した場合の換気量は、以下の式[29]のように簡略化されるため、その誤差を表す誤差比は式[30]、式[31]のようになる。
Q_{\mathrm{1}} = Q_{\mathrm{2}} = \alpha A \cdot \sqrt{\frac{\Delta \rho g h}{\rho_{\mathrm{o}}} } \; \cdots \; [29]\frac{Q_{\mathrm{1}}}{Q_{\mathrm{1}}'} = \sqrt{\frac{1}{2} \left ( \frac{\rho_{\mathrm{o}}}{\rho_{\mathrm{i}}}+1 \right )} \; \cdots \; [30]\frac{Q_{\mathrm{2}}}{Q_{\mathrm{2}}'} = \sqrt{\frac{1}{2} \frac{\rho_{\mathrm{o}}}{\rho_{\mathrm{i}}} \left ( 1 + \frac{\rho_{\mathrm{i}}}{\rho_{\mathrm{o}}} \right )} \; \cdots \; [31]例えば、Δρ/ρo=0.25（即ち、ρo/ρi=1.33）のように室内外の密度差が大きい場合（室内外温度差：約70°C）でもQ₁/Q₁’=1.08、Q₂/Q₂’=1.08となり、換気量の誤差は10%未満4[4] Poreh, M., and Hassid, S. 1982. Simulation of buoyancy and wind induced ventilation. Proceedings of the International Workshop on Wind Tunnel Modelling for Civil Engineering Applications, Gaithersburg, MD, Cambridge University Press, Cambridge.に抑えられる。
以上のことより、温度差換気量の計算において、室内外の空気密度の違いを考慮することは理論的には重要であるが、通常の温度差範囲では換気量への影響は小さく、実務上は密度を一様とする近似でも十分な精度が得られる。したがって、式[20]のような簡略化手法は、合理的なアプローチであると言える。
★ 以上の自然換気量の計算法に基づき、例題を解くことで深く学習したい方は下記のブログをご確認ください。
https://lee-lab.net/blog-contents-005
[1] Akins, R.E., J.A. Peterka, and J.E. Cermak. 1979. Averaged pressure coefficients for rectangular buildings. Wind Engineering: Proceedings of the Fifth International Conference, vol. 7, pp. 369-380.【PDF LINK】
[2] Swami, M.V., and S. Chandra. 1987. Procedures for calculating natural ventilation airflow rates in buildings. Final Report FSEC-CR-163-86. Florida Solar Energy Center, Cape Canaveral.【PDF LINK】
[3] Walker, I.S., and D.J. Wilson. 1994. Practical methods for improving estimates of natural ventilation rates. Proceedings of the 15th IEA Conference of the Air Infiltration and Ventilation Centre, Buxton, U.K., pp. 517-526.【PDF LINK】
[4] Poreh, M., and Hassid, S. 1982. Simulation of buoyancy and wind induced ventilation. Proceedings of the International Workshop on Wind Tunnel Modelling for Civil Engineering Applications, Gaithersburg, MD, Cambridge University Press, Cambridge.【PDF LINK】
Written by Sihwan Lee
[Associate Professor, Tokyo University of Science]